Research

Local superconducting states in unconventional superconductors

Non-reciprocal magnon propagation

Microwave non-reciprocity in Multiferroics

Local superconducting states in unconventional superconductors

[1] Y. Iguchi et al., Physical Review B (Letter) 103, L220503 (2021).

[2] I.P. Zheng, Y. Iguchi, et al., Physical Review B 100, 024514 (2019).

Reprinted figure from [1]. Copyright 2021, by American Physical Society.

Scanning SQUID (Superconducting QUantum Interference Device) microscopy, which can obtain the local susceptibility by measuring an absolute value of magnetic flux, is very unique and strong scanning magnetic probe. The purpose of this project is to reveal the local superconducting states of unconventional superconductors, such as chiral superconductor candidates, by using the scanning SQUID microscope.

1. Imaging isolated vortex dynamics

Scanning SQUID microscope can measure the superconducting vortex field in the magnetic flux san and the dynamics of vortex in the ac susceptibility scan. We directly measured the vortex dynamics in the nematic superconductor FeSe which has twin domains at low temperature, and visualized the anisotropic vortex pinning potential along the twin boundaries.[2]

Observed anisotropic vortex dynamics on FeSe (a) is captured by our simulation with anisotropic pinning potential (b). (c) is the difference of (a) and (b). Reprinted figure from [2]. Copyright 2019, by American Physical Society.

Vortices were pinned along the twin boundaries on FeSe(a). The local pinning potential is anisotropic along the twin boundaries(b). Reprinted figure from [2]. Copyright 2019, by American Physical Society.

We also measured the local vortex dynamics on a heavy fermion superconductor URu$_2$Si$_2$, which has twin domains under the strain, and observed the isotropic and anisotropic pinning potential at different locations of the same crystal.[1] The observed anisotropic pinning potentials on URu$_2$Si$_2$ didn't have a long range order in contrast to them on FeSe. Thus the local strain was dominant to break the rotational symmetry of the pinning potentials rather than electron nematic order (or the twin boundary if the sample forms it) on URu$_2$Si$_2$. In addition, we first estimated the temperature dependence of the local pinning force, $(1-(T/T_c)^2)^2$, by fitting the isotropic vortex dynamics on URu$_2$Si$_2$. This result suggested that the size of impurity in this sample is of the same order as the coherence length.

The observed vortex dynamics on URu$_2$Si$_2$(a),(b) are captured by our simulation with anisotropic (c) and isotropic (d) pinning potential, respectively. (e) The observed local anisotropy of pinning potential on URu$_2$Si$_2$ was not ordered. Reprinted figure from [1]. Copyright 2021, by American Physical Society.

The temperature dependence of the pinning force constant $k$ which was estimated from the vortex dynamics at three different locations on URu$_2$Si$_2$. Reprinted figure from [1]. Copyright 2021, by American Physical Society.

2. Local observation of superfluid density and spontaneous magnetism in chiral superconductor candidates

Chiral superconductivity is an intriguing quantum phenomenon where unconventional superconductors spontaneously develop an angular momentum breaking time-reversal symmetry. It is a non-trivial topological state, which may have spontaneous topological modes at surface or defects, such as chiral edge currents or Majorana zero modes. The observation of the time reversal symmetry breaking or Majorana zero modes have been reported in some superconductors. However no one still reported a decisive evidence for chiral superconductivity.

The heavy fermion superconductor URu$_2$Si$_2$ is a candidate for chiral, time-reversal symmetry-breaking superconductivity with a nodal gap structure. URu$_2$Si$_2$ has been extensively studied to reveal the unconventional superconducting state coexisting the novel hidden order state for a long time. However, the signatures of chirality and nodes appear in some crystals but not in others, raising questions about the true nature of the superconducting state.

In order to measure spontaneous magnetism and the superfluid density, we imaged the zero-field magnetic flux and the low-field diamagnetic response in URu$_2$Si$_2$ with micron-scale spatial resolution, using scanning SQUID microscopy. [1] We observed superconductivity ($T_{SC}$=1.5 K) and spatially inhomogeneous ferromagnetism ($T_{FM}$=16.1 K). At non-ferromagnetic area, however, no spontaneous magnetization expected for chiral superconductivity was detected. This result suggests that chirality either is not present or does not lead to detectable spontaneous magnetization.

The observed local negative susceptibility due to the Meissner effect (b ) and spontaneous ferromagnetic domains and vortices (c) on a single crystal of URu$_2$Si$_2$ (a). (d) The susceptibility on the ferromagnetic domain (P1) showed both phase transitions of ferromagnetic and superconducting, but the susceptibility observed far from ferromagnetic domains (P2) only showed the superconducting phase transition. Reprinted figure from [1]. Copyright 2021, by American Physical Society.

We also obtained linear-T superfluid density, which was estimated from the height dependence fo the local susceptibility at non-ferromagnetic area. These data support a nodal gap structure in URu$_2$Si$_2$.

The observed height $z$ dependence of the normalized susceptibility at several temperature on URu$_2$Si$_2$ depends on the London penetration depth. Reprinted figure from [1]. Copyright 2021, by American Physical Society.

The observed temperature dependence of the local London penetration depth (a) $\lambda$ estimated from the left figure and the local superfluid density $\lambda^2(0)/\lambda^2(T)$ (b), which is captured by the calculation with d-wave symmetry rather than s-wave. Reprinted figure from [1]. Copyright 2021, by American Physical Society.

Non-reciprocal magnon propagation

[1] Y. Iguchi, S. Uemura, K. Ueno, and Y. Onose, Physical Review B 92, 184419(2015).

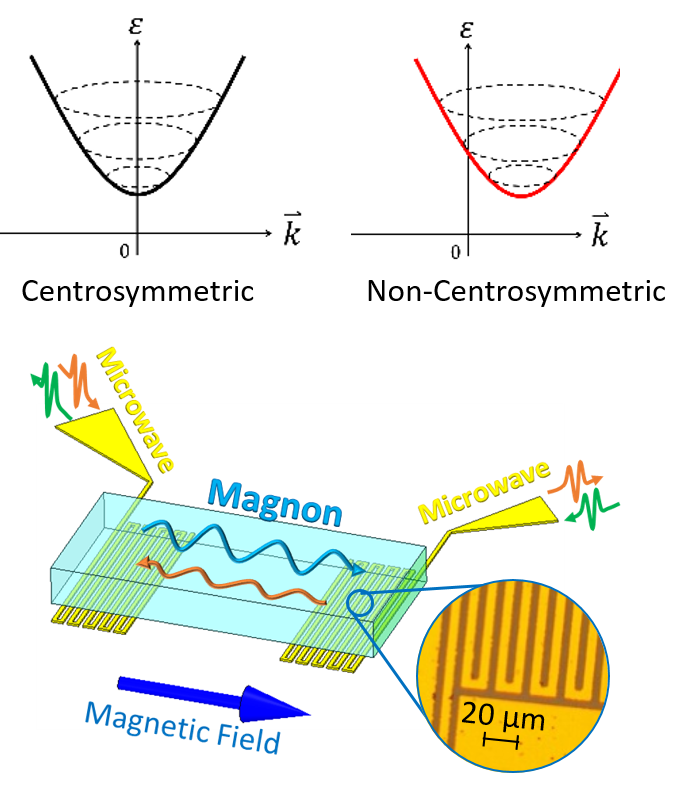
Spintronics and spin related physics have been attracting much attention recently. There are several important ingredients in this research field. Spin current is essential concept to understand spin transports in nano-scale magnetic devises such as the tunnel magnetoresistance (TMR) device. While the spin current is usually carried by electronic carriers, the spin current driven by magnetic excitations (magnons) is also important for spin transports in magnetic materials. Recently, numbers of novel phenomena related to the magnons have been reported, e.g. spin Seebeck effect, spin wave Doppler effect, and magnon Hall effect. Spintronics related to the magnons is denoted as "magnonics" and thought to be one of the priority research fields near future.

Relativistic spin-orbit interaction is another key ingredient. The spin Hall effect is induced by the spin-orbit interaction, which is useful conversion from charge current to spin current. The modification of band structure owing to the spin-orbit is also important. One of the examples is Rashba effect, which is the spin-splitting depending on the momentum direction. The Rashba spin-orbit interaction can be utilized for the spin field effect transistor.

We have reported that the non-reciprocal microwave response induced by the asymmetric magnon band in a non-centrosymmetric ferromagnet LiFe$_5$O$_8$, which originates from the relativistic Dzyaloshinskii-Moriya interaction. [1] This result clearly demonstrates that the concept of relativistic band modification is also applicable to magnons in ferromagnets, and useful for designing microwave devices.

Observed microwave transmittances owing to magnon propagation in LiFe$_5$O$_8$ and Y$_3$Fe$_5$O$_{12}$. The non-reciprocity was only observed in LiFe$_5$O$_8$ and reversed by reversing magnetic field. Reprinted figure from [1]. Copyright 2015, by American Physical Society.

Microwave non-reciprocity in Multiferroics

[1] Y. Iguchi, Y. Nii, and Y. Onose, Nature Communications 8, 15252(2017).

[2] Y. Iguchi et al., Physical Review B 98, 064416 (2018).

[3] S. Hirose, Y. Iguchi et al., Applied Physics Letters 121, 222401 (2022) [Editor's picks]

Macroscopic responses observed in solids have always been supported by the symmetry breaking in a state of matter. For example, piezoelectricity and natural optical activity emerge in spatial-inversion symmetry (SIS) broken materials. Time-reversal symmetry (TRS) breaking induces the Hall effect and Faraday effect. It turned out recently that there is a class of systems that require the breaking of both SIS and TRS in materials. The breakthrough is provided by the discovery of the magnetically induced ferroelectrics (multiferroics). Several developments followed such as magnetoelectric effect, a variation of the magnetization induced by the electric field and the electric polarization controlled by the magnetic field. The breaking of both SIS and TRS also affects the dynamics of elementary excitations; the energy and decay rate of wave vector $+k$ become not equivalent to those of $-k$. This phenomenon is non-reciprocity. The non-reciprocity is nontrivial, because the origin is intrinsic interactions appearing only in both SIS and TRS broken materials such as the spin-orbit interaction. We have focused on the non-reciprocal phenomena relevant to magnon excitation, and studied the non-reciprocity of the microwave near magnon excitation frequency in the non-centrosymmetric magnets.

1. Magnetoelectrical control of non-reciprocal microwave response in a multiferroic helimagnet

The non-reciprocity has been extensively investigated in visible, X-ray, terahertz, and microwave regions. We demonstrate, for the first time, the control of microwave non-reciprocity with use of external electric and magnetic fields in a multiferroic helimagnet [1]. In the microwave region, more conventional non-reciprocity can be induced by the asymmetric configuration of centrosymmetric ferromagnet in microwave circuits. This mechanism is utilized for important microwave components such isolators, in which the microwave propagation is forbidden in one direction but possible in the other. While the forbidden direction of commercial isolators cannot be changed after the fabrication, our result clearly shows that controllable isolators can be realized with use of a multiferroic helimagnet.

We demonstrated that the multiferroic helimagnet Ba$_2$Mg$_2$Fe$_{12}$O$_{22}$ has the conical magnon excitation in the microwave region.[1] In the microwave region, the type-II multiferroics Ba$_2$Mg$_2$Fe$_{12}$O$_{22}$ shows the optical magnetoelectric effect at 6 K. In addition, the amplitude and the sign of the non-reciprocity of microwave can be controlled by the poling electric field.

Reprinted figures from [1]. Copyright (C)2017, Rights Managed by Nature Publishing Group.

We also investigated the nonreciprocity of microwave absorption in the room temperature multiferroic helimagnet BaSrCo$_2$Fe$_{11}$AlO$_{22}$ [3]. We observed that nonreciprocal microwave absorption at 6-20 GHz at room temperature, the sign of which can be controlled by the poling electric field. Such microwave properties will open the avenue of practical applications for future wireless communications.

Reprinted figures from [3]. Copyright (C)2022 Author(s). Published under an exclusive license by AIP Publishing.

2. Microwave non-reciprocity of magnon excitations in a non-centrosymmetric antiferromagnet

Antiferromagnetic spintronics has been attracting much attention, because it does not have large magnetization and appropriate for nano-devices. In contrast to the magnon excitations in magnets with the finite magnetization, such as ferromagnets and conical magnets, the antiferromagnetic magnon excitation tends to need high frequency and high field for observation. In order to scrutinize the magnetic field dependent antiferromagnetic magnon modes and their non-reciprocal directional dichroism, here we chose Ba$_2$MnGe$_2$O$_7$, which has the low Néel temperature $T_N$ and small anisotropy, as a sample and have investigated the magnon excitations in the microwave region.[2]

The multiferroic antiferromagnet Ba$_2$MnGe$_2$O$_7$ has the conventional antiferromagnetic magnon modes with easy plane anisotropy in the microwave region. The fitting of experimentally observed magnetic field dependence of these modes to the theoretical equation provides the exchange interaction constant and the magnetic anisotropy of Ba$_2$MnGe$_2$O$_7$. We observed the microwave non-reciprocity of one of the magnon modes. The microwave non-reciprocity is quantitatively explained by using the spin wave theory, the Kubo formula, and the metal ligand hybridization mechanism.

Reprinted figure from [2]. Copyright 2018, by American Physical Society.